
Algo extraordinario ocurrió recientemente en el fútbol inglés. El Liverpool FC se coronó por segunda vez campeón de la Premier League. Sumado a sus 18 títulos anteriores a la Premier League, iguala el récord del Manchester United de ser campeón de Inglaterra en 20 ocasiones.
Pero mientras los seguidores del club celebraron este momento de triunfo, otra faceta asombrosa despertó la atención de los matemáticos.
Y es que la conquista del título por parte del Liverpool completó la apertura de una excepcional serie de números que lleva 33 años gestándose. La secuencia surge cuando clasificamos al Liverpool junto a los demás clubes que han ganado la Premier League desde su creación en 1992, enumerándolos por el número de títulos ganados, empezando por el más bajo.
Como se puede ver en la siguiente tabla, el número de títulos de la Premier League es el siguiente: 1, 1, 2, 3, 5, 8, 13.
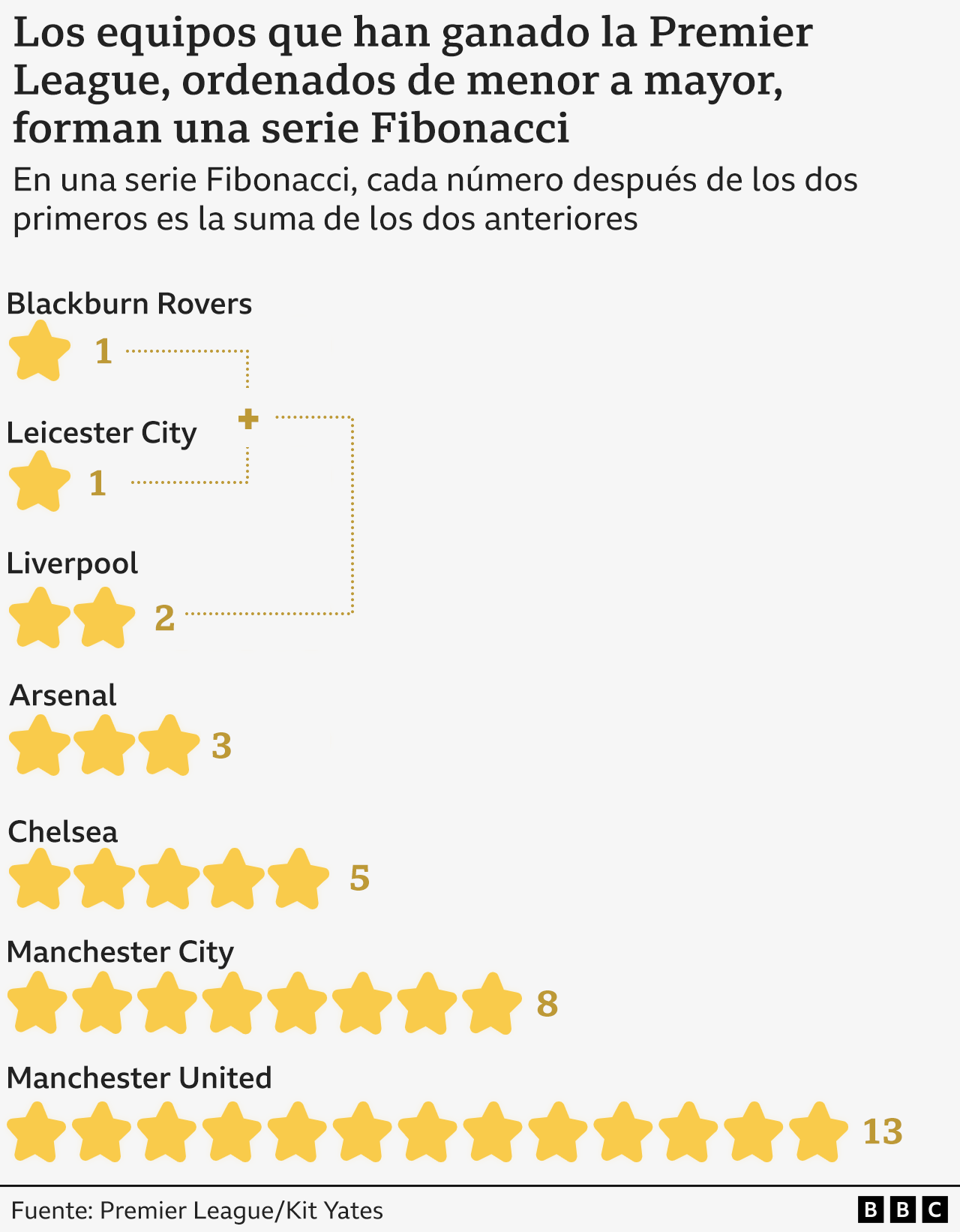
Para un ojo inexperto, esta secuencia puede no parecer significativa. Pero bastará para entusiasmar a muchos aficionados a las matemáticas. La reconocerán como la secuencia de Fibonacci, en la que cada número (después de los dos primeros) es la suma de los dos anteriores de la secuencia.
Esta secuencia se encuentra en una asombrosa variedad de lugares: desde las espirales de las semillas de los girasoles y las brácteas de las piñas hasta los patrones de los árboles genealógicos de algunas especies animales.
Las secuencias de Fibonacci (secuencias en plural porque si se parte de un par de números iniciales distintos y se sigue la regla de sumar números consecutivos para generar el siguiente se obtiene una secuencia distinta, pero relacionada) fueron introducidas por primera vez en la ciencia europea en 1202 por Leonardo de Pisa, también conocido por su apodo Fibonacci (que significa hijo de Bonaccio).
Sin embargo, mucho antes de que Fibonacci popularizara las secuencias en su libro "Liber Abaci", los matemáticos indios ya las conocían. Habían recurrido a las secuencias para ayudarles a enumerar el número de poemas posibles de una longitud determinada, utilizando sílabas cortas de una unidad de duración y sílabas largas de dos unidades de duración.

Los poetas/matemáticos indios sabían que se podía hacer un poema de longitud n tomando un poema de longitud n-1 y añadiendo una sílaba corta o un poema de longitud n-2 y añadiendo una sílaba larga. Por consiguiente, dedujeron que para calcular el número de poemas de una longitud determinada bastaba con sumar el número de poemas que tenían una sílaba menos y el número de poemas que tenían dos sílabas menos, la regla exacta que utilizamos hoy para definir una secuencia de Fibonacci.
Proporción áurea
En las secuencias se esconde otro pilar matemático importante y relacionado: la proporción áurea.
A medida que aumentan los términos de una secuencia de Fibonacci, la relación entre cada término y el anterior se acerca cada vez más a la proporción áurea, aproximada a 1,61803 por los primeros lugares de su expansión decimal.
Se cree que la proporción áurea rige la disposición de las hojas en el tallo de algunas especies de plantas y, supuestamente, produce resultados estéticamente agradables cuando se aplica al arte, la arquitectura y la música.
Los matemáticos suelen presentar las secuencias de Fibonacci como ejemplos de la belleza de las matemáticas. Pueden proporcionar ejemplos visuales vívidos de las matemáticas escritas en los patrones del mundo real, sin los cuales muchos no matemáticos pueden tener dificultades para entender la elegancia que vemos en nuestra materia.
Sin embargo, en nuestro exceso de proselitismo, existe la tentación de presentar las secuencias de Fibonacci o la proporción áurea como una especie de ley natural omnicomprensiva que rige fenómenos de varios órdenes de magnitud, desde las formas espirales de las conchas de los nautilos hasta los vórtices de los huracanes o los brazos curvos de las galaxias.

En realidad, aunque estas características naturales son estéticamente agradables, muy pocas de ellas se ajustan a las reglas de la secuencia de Fibonacci o presentan la proporción áurea.
Debemos tener cuidado de no intentar meter con calzador todos los patrones bellos en la delicada zapatilla de cristal de Fibonacci, para sugerir causalidad e imponer significado donde no lo hay.
¿Coincidencia?
Resulta extraordinario que la secuencia de Fibonacci aparezca en un lugar tan inesperado como la Premier League. Cuando, como científicos, observamos que una secuencia tan conocida como ésta aparece aparentemente de la nada, deberíamos empezar a preguntarnos si nos dice algo importante sobre el proceso que generó la secuencia.
¿Hay algún proceso sorprendente e invisible que subyace a las batallas por el título de la Premier League o no es más que una bonita coincidencia? Que veamos una secuencia de Fibonacci en algo no significa que esté ahí por alguna razón.

Sin embargo, detectar este tipo de coincidencias aparentes puede ser muy útil para el proceso de descubrimiento científico. En 1912, por ejemplo, Alfred Wegener observó la aparentemente extraña coincidencia de que la costa de África Occidental y la costa oriental de Sudamérica parecían encajar como las piezas de un rompecabezas.
A pesar de la opinión predominante en la época, según la cual las enormes masas de tierra de los continentes eran demasiado grandes para moverse, Wegener propuso la única teoría que conciliaba sus observaciones.
La deriva continental sugería que las masas de tierra no estaban arraigadas en su lugar, sino que podían, muy lentamente, cambiar sus posiciones relativas en la superficie de la Tierra.
Cuando Wegener publicó su teoría en 1915, se convirtió en el hazmerreír de todos.
Los geólogos rechazaron su extravagante idea, alegando la falta de un mecanismo para mover trozos tan enormes de la superficie terrestre, y tacharon de pura coincidencia la aparentemente ajustada teselación de los continentes.
Sin embargo, en la década de 1960, la teoría de la tectónica de placas -el movimiento del manto sólido y la corteza sobre la superficie terrestre- dio crédito a las teorías de Wegener, ahora ampliamente aceptadas.
La evolución de un error
Aunque las coincidencias pueden señalar el camino hacia nuevos descubrimientos científicos, también pueden suponer un obstáculo para el progreso científico cuando parecen confirmar una teoría incorrecta.
A principios del siglo XIX, el anatomista alemán Johann Friedrich Meckel cometió un error de este tipo. Meckel creía en la scala naturae (la escalera de la naturaleza), según la cual el ser humano está por encima del resto de los animales en una jerarquía ordenada pero estática.
Se suponía que las formas de vida más simples y primitivas se situaban en los peldaños más bajos de la escalera, mientras que los seres más complejos y avanzados residían en los más altos.
Sus puntos de vista no eran sorprendentes, dado que esta "gran cadena del ser" era la teoría predominante de la época. La teoría de la "descendencia común", hoy generalmente aceptada, según la cual múltiples especies descienden de una única población ancestral, era entonces una idea incipiente.
Meckel utilizó la scala naturae para formular una conjetura sobre su especialidad: el desarrollo embrionario.
Conocida como teoría de la recapitulación, postulaba que, a medida que se desarrollaban, los embriones de los animales de orden superior (como los mamíferos) progresaban sucesivamente a través de formas que se parecían mucho a los animales "menos perfectos", como los peces, los anfibios y los reptiles, situados en los peldaños inferiores de la escala.

Una predicción sorprendente, pero aparentemente improbable, de esta teoría era que, a medida que los humanos avanzaban por el "estadio de pez", sus embriones tendrían hendiduras branquiales.
En 1827 se descubrió que los embriones humanos tienen realmente hendiduras que se asemejan a branquias en una fase temprana del desarrollo. Este extraordinario hallazgo parecía confirmar la predicción de Meckel y corroborar su teoría de la recapitulación.
Hasta casi 50 años más tarde, en la década de 1870, la teoría de la recapitulación del desarrollo no se descartó definitivamente y la idea de la descendencia común empezó a imponerse.
La descendencia común es la base de lo que hoy conocemos como teoría evolutiva moderna. Dejó claro que, lejos de pasar por una "etapa de pez" en el útero, las hendiduras branquiales eran consecuencia del hecho de que, al compartir un antepasado común con los peces, también compartimos gran parte de su ADN y de sus primeros procesos de desarrollo.
A veces las coincidencias pueden llevar a los científicos por mal camino, pues parecen apuntar a una conclusión cuando, en realidad, hay una explicación alternativa para las observaciones que se apoya mejor en los hechos.
Entonces, ¿qué significa para el deporte rey el hecho de que la bella y casi mística secuencia de Fibonacci haya aparecido en los datos sobre el número de títulos de la Premier League ganados? Sin ningún mecanismo plausible que pueda haber dado lugar a la secuencia, la respuesta es casi con toda seguridad nada.
Es maravilloso haber descubierto esta secuencia matemática en un lugar tan insólito, lo que nos da la oportunidad de reflexionar sobre la importancia de los números de Fibonacci. Pero un patrón no siempre significa causalidad: una coincidencia a veces es sólo una coincidencia.
Y, al igual que las hendiduras branquiales de Meckel, su aparición en los récords de la Premier League no es más que eso: nada más que una coincidencia espectacular pero, en última instancia, engañosa.
*Este artículo fue publicado en BBC Future. Haz clic aquí para leer la versión original (en inglés).

Haz clic aquí para leer más historias de BBC News Mundo.
Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
También puedes seguirnos en YouTube, Instagram, TikTok, X, Facebook y en nuestro nuevo canal de WhatsApp, donde encontrarás noticias de última hora y nuestro mejor contenido.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.
- Qué es la serie de Fibonacci y qué tiene que ver con el número áureo
- Fibonacci, el matemático que se puso a contar conejos y descubrió la secuencia divina
- Cómo India hizo descubrimientos matemáticos por los que europeos se llevaron el crédito siglos después
!function(s,e,n,c,r){if(r=s._ns_bbcws=s._ns_bbcws||r,s[r]||(s[r+"_d"]=s[r+"_d"]||[],s[r]=function(){s[r+"_d"].push(arguments)},s[r].sources=[]),c&&s[r].sources.indexOf(c)<0){var t=e.createElement(n);t.async=1,t.src=c;var a=e.getElementsByTagName(n)[0];a.parentNode.insertBefore(t,a),s[r].sources.push(c)}}(window,document,"script","https://news.files.bbci.co.uk/ws/partner-analytics/js/fullTracker.min.js","s_bbcws");s_bbcws('syndSource','ISAPI');s_bbcws('orgUnit','ws');s_bbcws('platform','partner');s_bbcws('partner','acento.com.do');s_bbcws('producer','mundo');s_bbcws('language','es');s_bbcws('setStory', {'origin': 'optimo','guid': 'cqx41nnxy10o','assetType': 'article','pageCounter': 'mundo.articles.cqx41nnxy10o.page','title': 'Cómo el triunfo del Liverpool en la Premier League pone de manifiesto la serie de Fibonacci, una de las secuencias de números más famosas de la historia','author': 'Kit Yates – BBC Future*','published': '2025-05-03T09:24:01.126Z','updated': '2025-05-03T09:24:01.126Z'});s_bbcws('track','pageView');
Compartir esta nota